What is edge diffraction?
- Knife Edge Propagation
- Edge Diffraction Simulator
- Edge Diffraction Formula
- Speaker Edge Diffraction
- Knife Edge Diffraction Model
- Double Edge Diffraction
- Speaker Edge Diffraction
Free Download: The Edge program is a baffle diffraction simulator.
Information
Modeling of knife-edge diffraction using the GTD makes which is the well-known expression for knife-edge diffraction use of the general solution for wedge diffraction considering. The limits of validity of (1) and (5) are determined by the particular case of a wedge angle of 0. The diffraction by a half-plane edge is introduced. The description of the edge-diffraction experiment performed in the laboratory is given in Sec. 3, showing some of the outcomes obtained. Specifically, here we have used a razor blade to produce in the laboratory the edge. In optics, the Fresnel diffraction equation for near-field diffraction is an approximation of the Kirchhoff–Fresnel diffraction that can be applied to the propagation of waves in the near field. It is used to calculate the diffraction pattern created by waves passing through an aperture or around an object, when viewed from relatively close to the object.
Edge diffraction is the sound field component which must be added to the geometrical acoustics sound field to achieve the correct total sound field, for scattering from objects that consist of surfaces that are plane and rigid.
How can it be used?
In computational room acoustics, to improve the accuracy in general at low frequencies, or for stage reflectors, near balcony edges, and in orchestra pits [Svensson, Medwin, Torres 2000], [Torres, Svensson, Kleiner 2001].In studies of transducers (loudspeakers, microphones), in order to take the influence of the cabinet into account, [Vanderkooy 1991], [Svensson, Wendlandt 2000].
Scattering from rough surfaces, if these are modeled as deterministic 'wedge assemblages' [Keiffer, Novarini 2000].
Noise barriers - the classical edge diffraction problem [Maekawa 1968], [Medwin 1981].
Geophysics: reflections from wedge-shaped discontinuities between layers of different media [Trorey 1977].
Underwater acoustics: both surface scattering and for wedge-shaped discontinuities as above.
What analysis methods are available?
Frequency-domain methods: a large number of studies have developed exact (Macdonald 1915) and approximate methods for infinite edges. Examples of the latter are the Geometrical Theory of Diffraction (GTD), [Keller 1962], and the Uniform Asymptotic Theory of Diffraction (UATD), [Ahluwalia et al 1968]. Others can be found in [Maekawa 1968], [Bowman et al 1969], [Pierce 1974], [Kouyomjian, Pathak 1974], [Cox, Lam 1993].Time-domain methods: Biot-Tolstoy presented the time-domain solution for the infinite wedge in 1957. Later Medwin derived a 'Huygens interpretation' from this, which could be extended to finite wedges and multiple diffraction [Medwin 1982]. Svensson et al then derived an analytical directivity function for secondary edge sources, which gives the exact impulse response for finite wedges, even curved ones [Svensson et al 1999].
A classical method is based on the Kirchhoff diffraction approximation, which can give elegant time-domain line integral expression for the edge diffraction [Sakurai, Nagata 1981]. It is often believed to be asymptotically correct for high frequencies. However, as shown by Jebsen and Medwin, the Kirchhoff diffraction approximation is not asymptotically correct and it can give large errors at high frequencies [Jebsen, Medwin 1982].
Matlab toolbox for the time domain models of edge diffraction
A Matlab toolbox is available as free-ware for non-commercial use under www.tele.ntnu.no/users/svensson/Matlab.html. It calculate impulse responses including low-order specular reflections and edge diffraction for geometries defined in a simple CAD-format.
Example: Computational room acoustics
In room acoustics it is clear that geometrical acoustics models can work well at mid to high frequencies, especially if surface scattering is included, as shown by Round-Robin comparisons between computer predictions and measurements by M. Vorländer [Vorländer1995]. At low frequencies, however, geometrical acoustics is insufficient for accurate predictions. Also, near balcony edges and seat edges edge diffraction might be very significant also at higher frequencies as shown by R. Torres et al [Torres 1997] using auralization.One example of the edge diffraction method in room acoustic impulse response prediction is shown below: a simple model of a stage house [taken from Torres et al 2001]. A single source is placed on the stage, and there is a lateral array of 100 receiver positions in front of the stage. Impulse responses were calculated for these 100 receiver positions. The are plotted below, on top of each other but displaced vertically. Thereby the wavefronts are clearly visible. Results are shown for pure specular reflections, and with edge diffraction added. The impulse responses were low-pass filtered with a single Hanning window, corresponding to a cut-off frequency of approx. 350 Hz.
When only specular reflections are included, typical truncated wavefronts result. This means that as we move the receiver position just past the point where the image source becomes invisible, the reflection suddenly disappears. These truncated wavefronts are clearly unphysical. When the edge diffraction components are added, the wavefronts become perfectly smooth and continuous. Furthermore, there are more wavefield components since many diffraction or specular-diffraction combinations are possible.
Background/theory

H.Medwin used the exact Biot-Tolstoy solution to suggest an edge source interpretation of the edge diffraction phenomenon [Medwin 1981]. This was quite successful and gave very good agreement between calculations and measurements for many different cases. However, a theoretical derivation wasn't offered so the model was qualitatively reasonable but its quantitative accuracy was somewhat unsure. J.Vanderkooy explored an asymptotic frequency-domain formulation for the infinite wedge and managed to transform it into a very elegant and simple time-domain formulation. Comparisons with boundary element calculations for a point source on a rigid loudspeaker cabinet showed good agreement at mid and high frequencies but erroneous results at low frequencies, and including higher-order diffraction components did not improve the results [Vanderkooy 1991]. It had been shown already in the 20s that the so-called Maggi-Rubinowicz transformation when applied to the Kirchhoff approximation gives the scattering from a finite plane in terms of a line integral which is a very simple expression. This expression was exploited by Sakurai in the 80s [Sakurai and Nagata1981]. However, it was shown by Medwin and his colleagues that this Kirchhoff approximation leads to erroneous results both at low and high frequencies for certain radiation angles [Jebsen and Medwin 1982]. Consequently it is not suitable for general diffraction modelling.
In 1997, a new model was suggested by U. P. Svensson, R. I. Andersson (later R.I. Fred), and J. Vanderkooy for the finite wedge diffraction [Svensson et al 1997]. By assuming the existence of an analytic directivity function for edge sources along the edge of an infinite wedge, it was possible to derive the form of this directivity function. This can be seen as an analytic extension to the model used by Medwin et al. With access to such a directivity function, curved edges can be studied as well and very good agreement has been shown between the new method and accurate frequency-domain calculations for the axisymmetric backscattering of a circular thin disc. More about this new method can be read in [Svensson et al [1999] or [Torres et al 2001]. If you have problems to find these references, please contact svensson@tele.ntnu.no.
References to the new method by Svensson, Fred and Vanderkooy
Journal papers U. P. Svensson, R. I. Fred, J. Vanderkooy, 'Analytic secondary source model of edge diffraction impulse responses,' J. Acoust. Soc. Am., 106, 2331-2344 (1999).R. R. Torres, U. P. Svensson, M. Kleiner, 'Computation of edge diffraction for more accurate room acoustics auralization,' J. Acoust. Soc. Am., 109, 600-610 (2001).
Conference proceedings P. Svensson, R. Andersson, J. Vanderkooy, 'Time-domain approaches to the edge diffraction problem - applications to boxed loudspeakers,' presented at the Third Joint Meeting of the Acoustical Society of America and the Acoustical Society of Japan, J. Acoust. Soc. Am. (Abstracts) 100, 2749 (1996). No proceedings available.R. R. Torres, M. Kleiner, U. P. Svensson, 'Computation of impulse response for stage-house geometries with use of edge-diffraction models,' J. Acoust. Soc. Am. 101, 3134 (1997). (Abstracts).
U. P. Svensson, R. I. Andersson, J. Vanderkooy, 'A new interpretation of the edge diffraction phenomenon,' in Proceedings of the Autumn meeting of the Acoustical Society of Japan, Sapporo, Japan, Sept. 17-19, 813-814 (1997).
U. P. Svensson, R. I. Andersson, J. Vanderkooy, 'A time-domain model of edge diffraction based on the exact Biot-Tolstoy solution,' in the Technical Report of the Institute of Electronics, Information and Communication Engineers, EA97-39, Tokyo, Japan, Sept. 26, 9-16 (1997). (Contact the first author if you are interested in a copy of this paper)
R. R. Torres, M. Kleiner, 'Audibility of edge diffraction in auralization of a stage house,' J. Acoust. Soc. Am. 103, 2789 (1998). (Abstracts).
U. P. Svensson, R. Andersson, J. Vanderkooy, 'An analytical time-domain model of edge diffraction,' in Proceedings of NAM98, Nordic Acoustical Meeting, Stockholm, Sweden, Sept. 7-9, 269-272 (1998). (Contact the first author if you are interested in a copy of this paper)
U. P. Svensson, R. Andersson, J. Vanderkooy, 'An analytical decomposition of the Biot-Tolstoy edge diffraction model,' J. Acoust. Soc. Am. (Abstracts) 104, 1858 (1998).
R. R. Torres, M. Kleiner, 'Considerations for including surface scattering in room-acoustics auralization,' J. Acoust. Soc. Am. 105, 1198 (1999). (Abstracts).
U. P. Svensson, ' Modelling scattering impulse responses with analytic edge sources,' presented at the 23rd Scandinavian Symposium on Physical Acoustics, Ustaoset, Norway, Jan. 30 - Feb. 2 (2000). In Proc., 33-36, NTNU, Dept. of Telecommunications, Trondheim, Norway (2000).
P. Svensson, K. Wendlandt, U. Kristiansen, F. Goyard, P. Auguereau, 'Efficient method for calculating the sound radiation of vibrating structures,' pres. at Baltic Acoustic 2000, Vilnius, Lithuania, Sept. 17-21 (2000).
P. Svensson, K. Wendlandt, 'The influence of a loudspeaker cabinet's shape on the radiated power,' pres. at Baltic Acoustic 2000, Vilnius, Lithuania, Sept. 17-21 (2000).
Knife Edge Propagation
R. R. Torres, U. P. Svensson, M. Kleiner, 'Edge diffraction in room acoustics computations,' pres. at the EAA symposium on Architectural Acoustics, Madrid, Spain, Oct. 16-20 (2000).
U. P. Svensson, R. R. Torres, H. Medwin, 'The Color of Early Sound Arrivals in an Auditorium,' presented at the Joint Meeting: 140th Meeting of the Acoustical Society of America and Noise-Con 2000, Newport Beach, CA, USA, Dec. 3-8 (2000). J. Acoust. Soc. Am. (Abstracts) 108, 2648 (2000).
U. P. Svensson, 'Acoustic rendering beyond geometrical acoustics,' presented at the Campfire: Acoustic rendering for virtual environments, Snowbird, Utah, USA, May 26-29 (2001). Abstract on http://www.bell-labs.com/topic/conferences/campfire/program.html
R. R. Torres, M. Kleiner, U. P. Svensson, 'Edge diffraction and scattering in the early room impulse response,' presented at the 141st Meeting of the Acoust. Soc. Am., Chicaho, Illinois.
U. P. Svensson, L. Savioja, T. Lokki, U. R. Kristiansen, 'Low-frequency models for room acoustic prediction,' presented at the 17th International Congress on Acoustics, Rome, Italy, Sept. 2-7, (2001).
R. R. Torres, M. Vorländer, U. P. Svensson, M. Kleiner, 'Studies of scattering from faceted room surfaces,' presented at the 17th International Congress on Acoustics, Rome, Italy, Sept. 2-7, (2001).
Other references on edge diffraction, arranged by method
Papers by Biot and Tolstoy, and papers on Medwin's method M. A. Biot, I. Tolstoy, 'Formulation of wave propagation in infinite media by normal coordinates with an application to diffraction,' J. Acoust. Soc. Am. 29, 381-391 (1957).H. Medwin, 'Shadowing by finite noise barriers,' J. Acoust. Soc. Am. 69, 1060-64 (1981).
H. Medwin, E. Childs, G. M. Jebsen, 'Impulse studies of double diffraction: A discrete Huygens interpretation,' J. Acoust. Soc. Am. 72, 1005-1013 (1982).
G. M. Jebsen, H. Medwin, 'On the failure of the Kirchhoff assumption in backscatter,' J. Acoust. Soc. Am. 72, 1607-11 (1982).
C. S. Clay, W. A. Kinney, 'Numerical computations of time-domain diffractions from wedges and reflections from facets,' J. Acoust. Soc. Am. 83, 2126-2133 (1988). Misprints in eqs 24 and 25 and 16.
I. Tolstoy, 'Exact, explicit solutions for diffraction by hard sound barriers and seamounts,' J. Acoust. Soc. Am. 85, 661-669 (1989).
G. V. Norton, J. C. Novarini, R. S. Keiffer, 'An evaluation of the Kirchhoff approximation in predicting the axial impulse response of hard and soft disks,' J. Acoust. Soc. Am. 93, 3049-3056 (1993).
R. S. Keiffer, J. C. Novarini, G. V. Norton, 'The impulse response of an aperture: Numerical calculations within the framework of the wedge assemblage method,' J. Acoust. Soc. Am. 95, 3-12 (1994).
J. P. Chambers, Y. H. Berthelot, 'Time-domain experiments on the diffraction of sound by a step discontinuity,' J. Acoust. Soc. Am. 96, 1887-1892 (1994).
R. S. Keiffer, J. C. Novarini, 'A time domain rough surface scattering model based on wedge diffraction: Application to low-frequency backscattering from two-dimensional sea surfaces,' J. Acoust. Soc. Am. 107, 27-39 (2000).
The Kirchhoff diffraction approximation W. Trorey, 'A simple theory for seismic diffraction,' Geophysics 35, 762-784 (1970).F. J. Hilterman, 'Amplitude of seismic waves - a quick look,' Geophysics 40, 745-762 (1975).
J. R. Berryhill, 'Diffraction response for nonzero separation of source and receiver,' Geophysics 42, 1158-1176 (1977).
W. Trorey, 'Diffraction for arbitrary source receiver locations,' Geophysics 42, 1177-1182 (1977).
Y. Sakurai, K. Nagata, 'Sound reflections of a rigid plane and of the 'live end' composed by those panels,' J. Acoust. Soc. Jpn (E) 2, 5-14 (1981).
G. M. Jebsen, H. Medwin, 'On the failure of the Kirchhoff assumption in backscatter,' J. Acoust. Soc. Am. 72, 1607-11 (1982).
Y. Sakurai, K. Nagata, 'Practical estimation of sound reflection of a panel with a reflection coefficient,' J. Acoust. Soc. Jpn (E) 3, 7-19 (1982).
Y. Sakurai, K. Ishida, 'Multiple reflections between rigid plane panels,' J. Acoust. Soc. Jpn (E) 3, 183-190 (1982).
Vanderkooy's method J. Vanderkooy, 'A simple theory of cabinet edge diffraction,' J. Aud. Eng. Soc. 39, 923-933 (1991).S. Rasmussen, K. B. Rasmussen, 'On Loudspeaker Cabinet Diffraction,' J. Aud. Eng. Soc. 42, 147-150 (1994).
The Geometrical theory of diffraction (GTD) J. B. Keller, 'The geometrical theory of diffraction,' J. Opt. Soc. Am. 52, 116-130 (1962).D. L. Hutchins, R. G. Kouyomjian, 'Calculation of the field of a baffled array by the geometrical theory of diffraction,' J. Acoust. Soc. Am. 45, 485-492 (1969).
R. M. Bews, M. J. Hawksford, 'Application of the Geometric Theory of Diffraction at the Edges of Loudspeaker Baffles,' J. Aud. Eng. Soc. 34, 771-779 (1986).
Various frequency domain methods D. S. Ahluwalia, R. M. Lewis, J. Boersma, 'Uniform asymptotic theory of diffraction by a plane screen,' S.I.A.M. J. Appl. Math. 16, 783-807 (1968).Z. Maekawa, 'Noise reduction by screens,' Appl. Acoust. 1, 157-173 (1968).
J. J. Bowman, T. B. A. Senior, 'The wedge', Chap. 6 in ' Electromagnetic and acoustic scattering by simple shapes'. Eds. J. J. Bowman, T. B. A. Senior, P. L. E. Uslenghi, North-Holland, Amsterdam, (1969).
R. M. Lewis, J. Boersma, 'Uniform asymptotic theory of edge diffraction,' J. Math. Phys. 10, 2291-2305 (1969).
R. G. Kouyomjian, P. H. Pathak, 'A uniform geometrical theory of diffraction for an edge in a perfectly conducting surface,' Proc. of the IEEE 62, 1448-1461 (1974).
A. D. Pierce, 'Diffraction of sound around corners and over wide barriers,' J. Acoust. Soc. Am. 55, 941-955 (1974).
W J. Hadden, Jr., A. D. Pierce, 'Sound diffraction around screens and wedges for arbitrary point source locations,' J. Acoust. Soc. Am. 69, 1266-1276 (1981).
Erratum in J. Acoust. Soc. Am. 71(5). may (1982, p. 1290 98-06-14
P. Saha, A. D. Pierce, 'Geometrical theory of diffraction by an open rectangular box,' J. Acoust. Soc. Am. 75, 46-49 . (1984).
T. J. Cox, Y. W. Lam, 'Evaluation of Methods for Predicting the Scattering from Simple Rigid Panels,' Appl. Acoust. 40, 123-140 (1993).
K. B. Rasmussen, 'Model experiments related to outdoor propagation over an earth berm,' J. Acoust. Soc. Am. 96, 3617-3620 (1994).
Other references
M. Vorländer, 'International round robin on room acoustical computer simulations,' in Proc. of the Internat. Congress on Acoust., Trondheim, Norway, 26-30 June 1995, 689-692 (1995).B.-I. L. Dalenbäck, 'Room acoustic prediction based on a unified treatment of diffuse and specular reflection,' J. Acoust. Soc. Am. 100, 899-909 (1996).
The Fundementals
Edge Diffraction Simulator
IntroductionMaxwell's equationsPlane wavesFree space lossGas LossRefractionDiffractionReflectionsTroposcatterRain effectsVegetationStatisticsLink budgetsNoiseMultipathMeasurementsModelsDiffraction
Diffraction is the 'Bending' of wavefronts around obstacles. Diffraction occurs with all propagating waves, including sound waves, waves on water waves in materials and electromagnetic waves. Diffraction always occurs, its effects are generally only noticeable for waves where the wavelength similar to the size of the diffracting object.E.g. a Signal passing through a window
Diffraction is a large subject with some fairly difficult mathematics - we will try to limit the maths. What happens when an EM wave encounters a barrier?
Signals diffract around the barrier
The Huygens construction
Christiaan Huygens (1629–1695) was a Dutch mathematician, astronomer and physicist. He came up with a theory that light was a wave. His rule is 'Each point on a wavefront acts as a source of secondary wavelets. The combination of these secondary wavelets produces the new wavefront in the direction of propagation'. |
Diffraction over a perfectly absorbing knife edge can be understood through using Huygens construction:
The Cornu spiral is developed from Huygens, summing the amplitude and phase of each wavelet. To find the field at B from the wavefront A-A'
Sum the wavelets -2,-1,0,1,2 accounting for vector nature of the field.
Now move a knife edge upwards and it cuts out the lower wavelets, effectively cutting out the lower part of the spiral
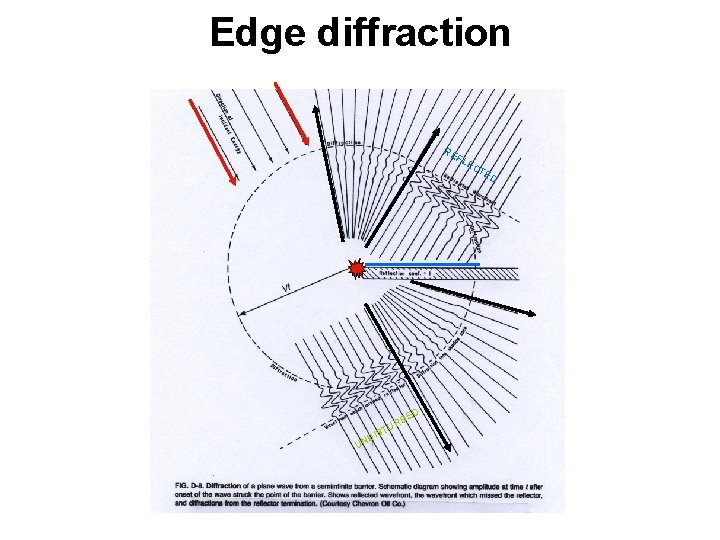
H.Medwin used the exact Biot-Tolstoy solution to suggest an edge source interpretation of the edge diffraction phenomenon [Medwin 1981]. This was quite successful and gave very good agreement between calculations and measurements for many different cases. However, a theoretical derivation wasn't offered so the model was qualitatively reasonable but its quantitative accuracy was somewhat unsure. J.Vanderkooy explored an asymptotic frequency-domain formulation for the infinite wedge and managed to transform it into a very elegant and simple time-domain formulation. Comparisons with boundary element calculations for a point source on a rigid loudspeaker cabinet showed good agreement at mid and high frequencies but erroneous results at low frequencies, and including higher-order diffraction components did not improve the results [Vanderkooy 1991]. It had been shown already in the 20s that the so-called Maggi-Rubinowicz transformation when applied to the Kirchhoff approximation gives the scattering from a finite plane in terms of a line integral which is a very simple expression. This expression was exploited by Sakurai in the 80s [Sakurai and Nagata1981]. However, it was shown by Medwin and his colleagues that this Kirchhoff approximation leads to erroneous results both at low and high frequencies for certain radiation angles [Jebsen and Medwin 1982]. Consequently it is not suitable for general diffraction modelling.
In 1997, a new model was suggested by U. P. Svensson, R. I. Andersson (later R.I. Fred), and J. Vanderkooy for the finite wedge diffraction [Svensson et al 1997]. By assuming the existence of an analytic directivity function for edge sources along the edge of an infinite wedge, it was possible to derive the form of this directivity function. This can be seen as an analytic extension to the model used by Medwin et al. With access to such a directivity function, curved edges can be studied as well and very good agreement has been shown between the new method and accurate frequency-domain calculations for the axisymmetric backscattering of a circular thin disc. More about this new method can be read in [Svensson et al [1999] or [Torres et al 2001]. If you have problems to find these references, please contact svensson@tele.ntnu.no.
References to the new method by Svensson, Fred and Vanderkooy
Journal papers U. P. Svensson, R. I. Fred, J. Vanderkooy, 'Analytic secondary source model of edge diffraction impulse responses,' J. Acoust. Soc. Am., 106, 2331-2344 (1999).R. R. Torres, U. P. Svensson, M. Kleiner, 'Computation of edge diffraction for more accurate room acoustics auralization,' J. Acoust. Soc. Am., 109, 600-610 (2001).
Conference proceedings P. Svensson, R. Andersson, J. Vanderkooy, 'Time-domain approaches to the edge diffraction problem - applications to boxed loudspeakers,' presented at the Third Joint Meeting of the Acoustical Society of America and the Acoustical Society of Japan, J. Acoust. Soc. Am. (Abstracts) 100, 2749 (1996). No proceedings available.R. R. Torres, M. Kleiner, U. P. Svensson, 'Computation of impulse response for stage-house geometries with use of edge-diffraction models,' J. Acoust. Soc. Am. 101, 3134 (1997). (Abstracts).
U. P. Svensson, R. I. Andersson, J. Vanderkooy, 'A new interpretation of the edge diffraction phenomenon,' in Proceedings of the Autumn meeting of the Acoustical Society of Japan, Sapporo, Japan, Sept. 17-19, 813-814 (1997).
U. P. Svensson, R. I. Andersson, J. Vanderkooy, 'A time-domain model of edge diffraction based on the exact Biot-Tolstoy solution,' in the Technical Report of the Institute of Electronics, Information and Communication Engineers, EA97-39, Tokyo, Japan, Sept. 26, 9-16 (1997). (Contact the first author if you are interested in a copy of this paper)
R. R. Torres, M. Kleiner, 'Audibility of edge diffraction in auralization of a stage house,' J. Acoust. Soc. Am. 103, 2789 (1998). (Abstracts).
U. P. Svensson, R. Andersson, J. Vanderkooy, 'An analytical time-domain model of edge diffraction,' in Proceedings of NAM98, Nordic Acoustical Meeting, Stockholm, Sweden, Sept. 7-9, 269-272 (1998). (Contact the first author if you are interested in a copy of this paper)
U. P. Svensson, R. Andersson, J. Vanderkooy, 'An analytical decomposition of the Biot-Tolstoy edge diffraction model,' J. Acoust. Soc. Am. (Abstracts) 104, 1858 (1998).
R. R. Torres, M. Kleiner, 'Considerations for including surface scattering in room-acoustics auralization,' J. Acoust. Soc. Am. 105, 1198 (1999). (Abstracts).
U. P. Svensson, ' Modelling scattering impulse responses with analytic edge sources,' presented at the 23rd Scandinavian Symposium on Physical Acoustics, Ustaoset, Norway, Jan. 30 - Feb. 2 (2000). In Proc., 33-36, NTNU, Dept. of Telecommunications, Trondheim, Norway (2000).
P. Svensson, K. Wendlandt, U. Kristiansen, F. Goyard, P. Auguereau, 'Efficient method for calculating the sound radiation of vibrating structures,' pres. at Baltic Acoustic 2000, Vilnius, Lithuania, Sept. 17-21 (2000).
P. Svensson, K. Wendlandt, 'The influence of a loudspeaker cabinet's shape on the radiated power,' pres. at Baltic Acoustic 2000, Vilnius, Lithuania, Sept. 17-21 (2000).
Knife Edge Propagation
R. R. Torres, U. P. Svensson, M. Kleiner, 'Edge diffraction in room acoustics computations,' pres. at the EAA symposium on Architectural Acoustics, Madrid, Spain, Oct. 16-20 (2000).
U. P. Svensson, R. R. Torres, H. Medwin, 'The Color of Early Sound Arrivals in an Auditorium,' presented at the Joint Meeting: 140th Meeting of the Acoustical Society of America and Noise-Con 2000, Newport Beach, CA, USA, Dec. 3-8 (2000). J. Acoust. Soc. Am. (Abstracts) 108, 2648 (2000).
U. P. Svensson, 'Acoustic rendering beyond geometrical acoustics,' presented at the Campfire: Acoustic rendering for virtual environments, Snowbird, Utah, USA, May 26-29 (2001). Abstract on http://www.bell-labs.com/topic/conferences/campfire/program.html
R. R. Torres, M. Kleiner, U. P. Svensson, 'Edge diffraction and scattering in the early room impulse response,' presented at the 141st Meeting of the Acoust. Soc. Am., Chicaho, Illinois.
U. P. Svensson, L. Savioja, T. Lokki, U. R. Kristiansen, 'Low-frequency models for room acoustic prediction,' presented at the 17th International Congress on Acoustics, Rome, Italy, Sept. 2-7, (2001).
R. R. Torres, M. Vorländer, U. P. Svensson, M. Kleiner, 'Studies of scattering from faceted room surfaces,' presented at the 17th International Congress on Acoustics, Rome, Italy, Sept. 2-7, (2001).
Other references on edge diffraction, arranged by method
Papers by Biot and Tolstoy, and papers on Medwin's method M. A. Biot, I. Tolstoy, 'Formulation of wave propagation in infinite media by normal coordinates with an application to diffraction,' J. Acoust. Soc. Am. 29, 381-391 (1957).H. Medwin, 'Shadowing by finite noise barriers,' J. Acoust. Soc. Am. 69, 1060-64 (1981).
H. Medwin, E. Childs, G. M. Jebsen, 'Impulse studies of double diffraction: A discrete Huygens interpretation,' J. Acoust. Soc. Am. 72, 1005-1013 (1982).
G. M. Jebsen, H. Medwin, 'On the failure of the Kirchhoff assumption in backscatter,' J. Acoust. Soc. Am. 72, 1607-11 (1982).
C. S. Clay, W. A. Kinney, 'Numerical computations of time-domain diffractions from wedges and reflections from facets,' J. Acoust. Soc. Am. 83, 2126-2133 (1988). Misprints in eqs 24 and 25 and 16.
I. Tolstoy, 'Exact, explicit solutions for diffraction by hard sound barriers and seamounts,' J. Acoust. Soc. Am. 85, 661-669 (1989).
G. V. Norton, J. C. Novarini, R. S. Keiffer, 'An evaluation of the Kirchhoff approximation in predicting the axial impulse response of hard and soft disks,' J. Acoust. Soc. Am. 93, 3049-3056 (1993).
R. S. Keiffer, J. C. Novarini, G. V. Norton, 'The impulse response of an aperture: Numerical calculations within the framework of the wedge assemblage method,' J. Acoust. Soc. Am. 95, 3-12 (1994).
J. P. Chambers, Y. H. Berthelot, 'Time-domain experiments on the diffraction of sound by a step discontinuity,' J. Acoust. Soc. Am. 96, 1887-1892 (1994).
R. S. Keiffer, J. C. Novarini, 'A time domain rough surface scattering model based on wedge diffraction: Application to low-frequency backscattering from two-dimensional sea surfaces,' J. Acoust. Soc. Am. 107, 27-39 (2000).
The Kirchhoff diffraction approximation W. Trorey, 'A simple theory for seismic diffraction,' Geophysics 35, 762-784 (1970).F. J. Hilterman, 'Amplitude of seismic waves - a quick look,' Geophysics 40, 745-762 (1975).
J. R. Berryhill, 'Diffraction response for nonzero separation of source and receiver,' Geophysics 42, 1158-1176 (1977).
W. Trorey, 'Diffraction for arbitrary source receiver locations,' Geophysics 42, 1177-1182 (1977).
Y. Sakurai, K. Nagata, 'Sound reflections of a rigid plane and of the 'live end' composed by those panels,' J. Acoust. Soc. Jpn (E) 2, 5-14 (1981).
G. M. Jebsen, H. Medwin, 'On the failure of the Kirchhoff assumption in backscatter,' J. Acoust. Soc. Am. 72, 1607-11 (1982).
Y. Sakurai, K. Nagata, 'Practical estimation of sound reflection of a panel with a reflection coefficient,' J. Acoust. Soc. Jpn (E) 3, 7-19 (1982).
Y. Sakurai, K. Ishida, 'Multiple reflections between rigid plane panels,' J. Acoust. Soc. Jpn (E) 3, 183-190 (1982).
Vanderkooy's method J. Vanderkooy, 'A simple theory of cabinet edge diffraction,' J. Aud. Eng. Soc. 39, 923-933 (1991).S. Rasmussen, K. B. Rasmussen, 'On Loudspeaker Cabinet Diffraction,' J. Aud. Eng. Soc. 42, 147-150 (1994).
The Geometrical theory of diffraction (GTD) J. B. Keller, 'The geometrical theory of diffraction,' J. Opt. Soc. Am. 52, 116-130 (1962).D. L. Hutchins, R. G. Kouyomjian, 'Calculation of the field of a baffled array by the geometrical theory of diffraction,' J. Acoust. Soc. Am. 45, 485-492 (1969).
R. M. Bews, M. J. Hawksford, 'Application of the Geometric Theory of Diffraction at the Edges of Loudspeaker Baffles,' J. Aud. Eng. Soc. 34, 771-779 (1986).
Various frequency domain methods D. S. Ahluwalia, R. M. Lewis, J. Boersma, 'Uniform asymptotic theory of diffraction by a plane screen,' S.I.A.M. J. Appl. Math. 16, 783-807 (1968).Z. Maekawa, 'Noise reduction by screens,' Appl. Acoust. 1, 157-173 (1968).
J. J. Bowman, T. B. A. Senior, 'The wedge', Chap. 6 in ' Electromagnetic and acoustic scattering by simple shapes'. Eds. J. J. Bowman, T. B. A. Senior, P. L. E. Uslenghi, North-Holland, Amsterdam, (1969).
R. M. Lewis, J. Boersma, 'Uniform asymptotic theory of edge diffraction,' J. Math. Phys. 10, 2291-2305 (1969).
R. G. Kouyomjian, P. H. Pathak, 'A uniform geometrical theory of diffraction for an edge in a perfectly conducting surface,' Proc. of the IEEE 62, 1448-1461 (1974).
A. D. Pierce, 'Diffraction of sound around corners and over wide barriers,' J. Acoust. Soc. Am. 55, 941-955 (1974).
W J. Hadden, Jr., A. D. Pierce, 'Sound diffraction around screens and wedges for arbitrary point source locations,' J. Acoust. Soc. Am. 69, 1266-1276 (1981).
Erratum in J. Acoust. Soc. Am. 71(5). may (1982, p. 1290 98-06-14
P. Saha, A. D. Pierce, 'Geometrical theory of diffraction by an open rectangular box,' J. Acoust. Soc. Am. 75, 46-49 . (1984).
T. J. Cox, Y. W. Lam, 'Evaluation of Methods for Predicting the Scattering from Simple Rigid Panels,' Appl. Acoust. 40, 123-140 (1993).
K. B. Rasmussen, 'Model experiments related to outdoor propagation over an earth berm,' J. Acoust. Soc. Am. 96, 3617-3620 (1994).
Other references
M. Vorländer, 'International round robin on room acoustical computer simulations,' in Proc. of the Internat. Congress on Acoust., Trondheim, Norway, 26-30 June 1995, 689-692 (1995).B.-I. L. Dalenbäck, 'Room acoustic prediction based on a unified treatment of diffuse and specular reflection,' J. Acoust. Soc. Am. 100, 899-909 (1996).
The Fundementals
Edge Diffraction Simulator
IntroductionMaxwell's equationsPlane wavesFree space lossGas LossRefractionDiffractionReflectionsTroposcatterRain effectsVegetationStatisticsLink budgetsNoiseMultipathMeasurementsModelsDiffraction
Diffraction is the 'Bending' of wavefronts around obstacles. Diffraction occurs with all propagating waves, including sound waves, waves on water waves in materials and electromagnetic waves. Diffraction always occurs, its effects are generally only noticeable for waves where the wavelength similar to the size of the diffracting object.E.g. a Signal passing through a window
Diffraction is a large subject with some fairly difficult mathematics - we will try to limit the maths. What happens when an EM wave encounters a barrier?
Signals diffract around the barrier
The Huygens construction
Christiaan Huygens (1629–1695) was a Dutch mathematician, astronomer and physicist. He came up with a theory that light was a wave. His rule is 'Each point on a wavefront acts as a source of secondary wavelets. The combination of these secondary wavelets produces the new wavefront in the direction of propagation'. |
Diffraction over a perfectly absorbing knife edge can be understood through using Huygens construction:
The Cornu spiral is developed from Huygens, summing the amplitude and phase of each wavelet. To find the field at B from the wavefront A-A'
Sum the wavelets -2,-1,0,1,2 accounting for vector nature of the field.
Now move a knife edge upwards and it cuts out the lower wavelets, effectively cutting out the lower part of the spiral
The effect of this is initially an oscillation then as the direct path is cut off, a signal loss.
Estimating the diffraction loss
Consider this geometry of a Knife edge gradually cutting off the wavefront. Also h << d1, d2 and λ<< d1,d2
Edge Diffraction Formula
Define parameter v:
Be careful with the sign if you use this last one, v is negative when edge is below the direct path.
The Cornu spiral is given to a good approximation by plotting the Fresnel Sine and Cosine integrals of v, where:
The E field can be expressed by summing from the top of the knife edge to infinity.
Speaker Edge Diffraction
..Which is beyond this tutorial…but can be written as:
Which we could work out but fortunately there is a very good approximation:
Here it is plotted:
Note: For a grazing knife edge, h = 0 so v = 0, giving a 6 dB loss. For first Fresnel zone clearance, v < -1.4, no loss).
Fresnel zones
I have mentioned these several times so I had better define them. From diffraction theory, it is clear that the effect of the knife edge begins before the direct path is cut. Some clearance is needed and the amount is expressed in terms of Fresnel zones. The first Fresnel zone is the locus of points where the additional path length compared with the shortest path does not exceed λ/2.
Further Fresnel zones are defined by additional 1/2 wavelength path length increments.
Line of Sight?
We generally assume line of sight clearance if more than 0.6 of the 1st Fresnel zone diameter is cleared.
Calculating Knife edge losses over the Earth
It is necessary to account for the curvature of the earth and for any slope in the path to calculate how far a knife edge impinges on a path. We do this by defining everything relative to a reference plane.
As long as the path length is much greater than the height of the obstacle, which it usually is, we can make an approximation for the height of the edge above the reference plane. It is this height that is used in the diffraction calculation.
So the diffraction parameter v is given by:
Knife Edge Diffraction Model
Which can be used to calculate the path loss from the equation for J(v)
Multiple Edges
What should we do if there is more than one obstruction? There are several models commonly used, including those by Bullington, Epstein-Petersen, Deygout, etc. They are all approximations and have potential for errors, especially with closely spaced edges. They differ in how they calculate the geometry and hence the parameter v and they differ in how many edges they take into account and how they add up the loses.
Bullington
The Bullington method is quite simple, it is based on constructing an equivalent single knife edge at the intersection of Tx/Rx 'horizons' and calculating the loss based on that. It is easy to do but is prone to underestimate loss as it can ignore important intermediate edges.
Epstein-Peterson
Sums up the loss for each single edge in turn, using height above dotted line as the effective height of edge. Potentially a better method but causes large errors on paths with closely spaced edges.
Deygout000b(the principle edge method)
This method is more involved, it splits the path into segments. Firstly we need to find edge with largest value of parameter v, ignoring all other edges. This is called the 'Principle Edge' and its v parameter is saved.
Now working from the principle edge P, we treat as if there is a new path between the TX and the principle edge and create a new reference plane and calculate v for the intermediate edge, if there is one, based on the height above the reference plane.
This edge will have a lower value of v and becomes the principle edge for the path from Tx to P. The process is recursive for multiple intermediate edges and can be repeated until all edges are considered. The method ignore any edges with 1st Fresnel zone clearance. The same process is used along the path from P to the receiver.
At the end of the procedure we will have a set of J(v) losses for each edge - the method simply adds these up. So for 3 edges:
Generally, modified Deygout methods are used with fudge factors and scaling factors to further improve the accuracy compared to measurements.
Real Terrain
Normal terrain, hills etc do not really look like knife edges and is often better represented by cylinders, which have a higher loss.
Double Edge Diffraction
Fortunately, we can approximate the additional loss, L = J(v) + T where T is an additional loss that accounts for diffraction at the tangents to the cylinder.
Most real-world obstructions are not like knife edges and it is only possible to solve the equations for idealised cases. Solutions for many objects and including reflection effects, loss from trees etc. rapidly become impractical and in many cases. Usually we do not really know enough detail about the exact nature of the terrain anyway. For example mobile systems would need re-analysing every 0.1 wavelengths and for 3G systems that would require a terrain map with points every 1.5cm. To overcome this and make a best guess, path loss prediction models are used, we will come on to these later.
Next
Speaker Edge Diffraction
© Mike Willis May 5th, 2007

